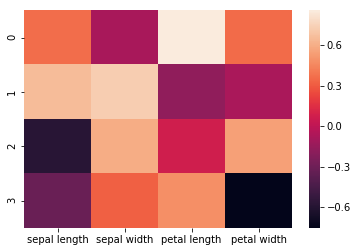沧海拾珠

机器学习之主成分分析（PCA）

发表于 | 分类于 |

1. 主成分分析Principla Component Analysis(PCA)

主成分分析是一种降维方法。主成分分析Principal component analysis(PCA)也称主分量分析，旨在利用降维的思想，把多维指标转化为少数几个综合维度，然后利用这些综合维度进行数据挖掘和学习，以代替原来利用所有维度进行挖掘学习的方法。

主成分分析的基本方法是按照一定的数学变换方法，把给定的一组相关变量（维度）通过线性变换转成另一组不相关的变量，这些新的变量按照方差依次递减的顺序排列。在数学变换中保持变量的总方差不变，使第一变量具有最大的方差，称为第一主成分，第二变量的方差次大，并且和第一变量不相关，称为第二主成分，依次类推。

2. 降维说明

假设原始数据集中有10个维度分别是tenure、cardmon、lncardmon、cardten、lncardten、wiremon、lnwiremon、wireten、lnwireten、hourstv，现在用主成分分析进行降维，降维后的每个“因子”是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
方程式用于 主成分-1
    0.006831 * tenure +
    0.007453 * cardmon +
    0.1861 * lncardmon +
    0.0001897 * cardten +
    0.1338 * lncardten +
    0.007552 * wiremon +
    0.3688 * lnwiremon +
    0.0001155 * wireten +
    0.132 * lnwireten +
    0.00006106 * hourstv +
    + -4.767
方程式用于 主成分-2
    -0.005607 * tenure +
    0.03288 * cardmon +
    0.759 * lncardmon +
    0.0002219 * cardten +
    0.05385 * lncardten +
    -0.01013 * wiremon +
    -0.4433 * lnwiremon +
    -0.0001222 * wireten +
    -0.1354 * lnwireten +
    0.008099 * hourstv +
    + -0.272
方程式用于 主成分-3
    -0.01809 * tenure +
    0.0124 * cardmon +
    0.2859 * lncardmon +
    -0.0002123 * cardten +
    -0.2252 * lncardten +
    0.0287 * wiremon +
    1.193 * lnwiremon +
    0.00002565 * wireten +
    -0.1644 * lnwireten +
    0.03984 * hourstv +
    + -4.076

这就是主成分分析后提取的3个能代表原始10个维度的新“维度”。通过上述结果我们可以发现主成分（也就是新的“维度”）是一个线性方程，而且是多元一次的方程。PCA可以对主成分分析的结果按重要性排序并根据用户需求只选择能代表大多数（甚至全部，如果你愿意）指标意义的成分，从而达到降维从而简化模型或是进行数据压缩的效果。

3. Iris 数据集分析。

用Python的机器学习库SKlearn中的PCA来对数据进行降维。原始数据集中有4个维度，现在要通过PCA转换成2个维度。

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn import datasets   
from sklearn.decomposition import PCA   
 
iris = datasets.load_iris() #导入iris数据集  
X = iris.data   
print ('first 5 raw samples:', X[:5])  
pca = PCA(n_components=2) # PCA算法中所要保留的主成分个数n，也即保留下来的特征个数n   
X_r = pca.fit_transform(X) # 用X来训练PCA模型，同时返回降维后的数据。  
print ('First 5 transformed samples:', X_r[:5])   
print ('Variance ratio:', pca.explained_variance_ratio_) 
# explained_variance_ratio_：返回所保留的n个成分各自的方差百分比。

结果如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
First 5 raw samples:
[[ 5.1  3.5  1.4  0.2]
 [ 4.9  3.   1.4  0.2]
 [ 4.7  3.2  1.3  0.2]
 [ 4.6  3.1  1.5  0.2]
 [ 5.   3.6  1.4  0.2]]
First 5 transformed samples: 
[[-2.68420713  0.32660731]
 [-2.71539062 -0.16955685]
 [-2.88981954 -0.13734561]
 [-2.7464372  -0.31112432]
 [-2.72859298  0.33392456]]
Variance ratio: [ 0.92461621  0.05301557]

PCA能找到代表原始数据最大特征的几个主成分。通过pca.explained_varianceratio可查看每个主成分能表达原始数据的方差。这里因为设置了n_components = 2，所以只能看到前两个成分的所占方差百分比，由数据可知，这两个成分的方差比例达到97%，意味着它们可以代表原始数据集95%的特征值。

PCA的应用是降维，用在所有大量数据集建模处理之前的降维过程，因此它是数据预处理过程的一步。

4. 可视化处理。

通过降维，可以把高纬度下无法做出来的图在二维或三维平面上显示出来，这也是PCA的一个非常重要的应用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
plt.figure()
colors = ['navy', 'turquoise', 'darkorange']
lw = 2
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(iris_df[y ==i,0], iris_df[y == i, 1], color=color, alpha=.8, lw=lw,
                label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of IRIS dataset')
# [y ==i,0]中，y==i 得到的是一个True/False列表，0 表示iris_df中的元素的第一个值。

结果如图所示：
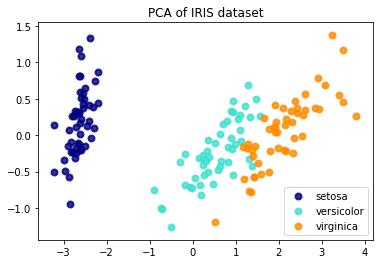
20180708_PCA

5.相关性分析。

主成分与 ‘sepal length’,’sepal width’,’petal length’,’petal width’ 这四个特征值的正负相关性可以通过pca.components_来查看。

1
2
3
4
5
6
7
pca = decomposition.PCA() #这里不设定n_components，表示所有成分被保留，有4个主成分。
iris_pca = pca.fit_transform(X)
print(pca.explained_variance_ratio_)
comps = pd.DataFrame(pca.components_, columns= ['sepal length','sepal width','petal length','petal width'])
from tabulate import tabulate
print(tabulate(comps, tablefmt="markdown", headers="keys"))
1
2
3
4
5
6
7
8
array([ 0.92461872,  0.05306648,  0.01710261,  0.00521218])
 sepal length    sepal width    petal length    petal width
--  --------------  -------------  --------------  -------------
 0        0.361387     -0.0845225       0.856671        0.358289
 1        0.656589      0.730161       -0.173373       -0.075481
 2       -0.58203       0.597911        0.0762361       0.545831
 3       -0.315487      0.319723        0.479839       -0.753657

制作heatmap图。

1
2
import seaborn as sb
sb.heatmap(comps)

结果如图所示：主成分1（y轴为0）和petal length 呈强正相关，主成分2（y轴为1）和sepal lenght, sepal width呈正相关。
20180708_heatmap